What are Quantum Random Number Generators
Random Number Generators (RNG) produce sequences of random numbers. Random numbers are essential for a number of applications: encrypted data transmission uses random numbers as secret keys, gambling machines need them, some numerical methods rely on them, and Quantum Key Distribution also requires them. Note that these applications have different requirements for the random numbers. In all applications, the random numbers have to be unpredictable and uni-formly distributed. If the random numbers are known, this is not a problem for some applications but certainly if they are used as secret keys. Unpredictability refers to the fact that if you know the past and the current state of a RNG, you are still unable to predict anything about the next pro-duced random number. To certify that an RNG produces an unpredictable random number se-quence is very challenging. Given a finite-length output of an RNG, such a proof (by statistical means) is impossible. A model of the internal function principle of an RNG is more effective.
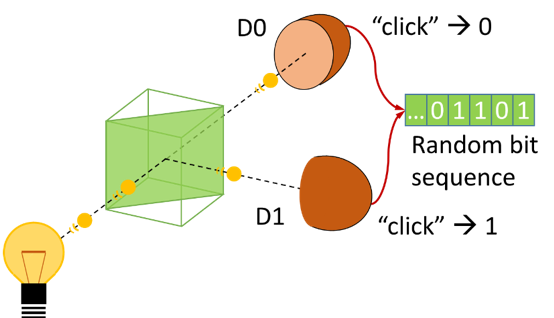
Concept for a Quantum Random Number Generator
There are three distinct types of random number generators (RNG): Pseudo-RNGs, True RNGs, and Quantum RNGs.
Pseudo-RNGs are deterministic mathematical algorithms that basically “expand” a given random seed to a much longer sequence of random numbers. The random seed is supposed to be “real randomness” and in a PC for instance obtained from mouse movement. In comparison to the other RNG types, a Pseudo-RNG is very cheap. However, the origin of the random seed is not standard-ized (and therefore of questionable reliability), not portable, and, hence, not suitable for high-quality cryptography. Pseudo-RNGs are gradually being replaced by True RNGs or QRNGs.
Both, TRNGs and QRNGs produce random numbers from the results of physical processes. Random number sequences gained in this way always have a particular level of predictability, they are not ideal. Applying randomness extraction to a non-ideal random num-ber sequence produces an ideal (albeit shorter) random number sequence. To apply randomness extraction, an upper bound for the amount of predictability has to be estimated. There are basically three methods to achieve this. First, a sophisticated model of the device, including all relevant non-idealities (like detectors with limited efficiency), which is difficult. An alternative are the self-testing QRNGs or device-independent QRNGs which on-line can determine the bound.
True RNGs (TRNG) take their random numbers from classical physical processes which, for all practi-cal purposes, are unpredictable. The unpredictability may be caused by many uncontrollable de-grees of freedom (e.g. noise) or systems with chaotic behaviour (like throwing a dice). TRNGs based on noise in electronic circuits are very cheap and small. The downside is that the quality of the random numbers produced by TRNGs is questionable and difficult to assess. It is a huge chal-lenge to construct a good TRNG and practically impossible to certify it. For that reason, TRNGs often involve a complex post-processing of the random numbers which makes them similar to Pseudo-RNGs. Also, there are known attacks to TRNGs.
QRNGs pull their random numbers from inherently indeterministic quantum processes. The inabil-ity to predict the numbers is not just based on complexity but it is in principle impossible to predict random numbers that are produced by QRNGs – one could say that even nature does not know these random numbers before they are produced. Figure 1 shows a prototypical QRNG. A photon impinges on a symmetrical beam splitter and after the beam splitter it is in a quantum mechanical superposition of “having been transmitted” and “having been reflected”. Eventually, a random one of the detectors D0 and D1 detects it and produces a random bit. QRNGs have many advantages: exploiting the objective randomness of nature and a relatively easy function principle. Hence, it is feasible to make a realistic physical model of a QRNG which can be the basis to certify the produced random numbers. A QRNG has a high attack resistance and usually the post-processing (randomness extraction) is conceptually easy. However, it is challenging to make a small and cheap or a real-ly fast QRNG.
